Симуляция слияния черных дыр GW150914

Проверка справедливости Общей теории относительности (ОТО) для сильных гравитационных полей — одна из важнейших и сложнейших задач современной экспериментальной гравитационной физики. Проблем на этом пути много, но одна из основных заключается в том, что гравитационные поля подавляющего большинства доступных для наблюдения космических объектов сравнительно слабы. Главным источником сильных гравитационных полей являются черные дыры, «прямое» исследование которых до недавнего времени было невозможно. Но в 2015 году ученым удалось «поймать» гравитационно-волновую рябь от слияния двух черных дыр, а в 2019 году — «сфотографировать» ближайшие окрестности сверхмассивной черной дыры в центре галактики M87 и запечатлеть ее «тень» на аккреционном диске. Сейчас счет зарегистрированных слияний черных дыр идет уже на десятки, так что у ученых нет недостатка в данных. Но продолжается анализ и самого первого зарегистрированного слияния: американские астрофизики смогли определить площадь горизонтов событий участвовавших в нем черных дыр и показали, что площадь горизонта образовавшейся в результате слияния дыры превышает сумму площадей горизонтов двух исходных дыр. Таким образом, они подтвердили сформулированное Стивеном Хокингом следствие из уравнений ОТО, согласно которому площадь горизонтов черных дыр не может уменьшаться с ходом времени. Это следствие во многих отношениях аналогично второму началу термодинамики для черных дыр.

Существование черных дыр является одним из важнейших предсказаний Общей теории относительности (ОТО), представляющей собой релятивистскую теорию гравитации, обобщающую закон тяготения Ньютона на случай сильных гравитационных полей и высоких (то есть сравнимых со скоростью света) скоростей движения взаимодействующих объектов. ОТО, построенная Альбертом Эйнштейном в 1915–1916 годах (подробнее об истории этой теории читайте в новости Столетие ОТО, или Юбилей «Первой ноябрьской революции», «Элементы», 25.11.2015), является геометрической теорией гравитации. Это означает, что она интерпретирует гравитационные силы как изменение геометрии пространства-времени, вызванное наличием в нем материи и полей.

Согласно ОТО, черная дыра представляет собой точку бесконечной плотности, но конечной полной массы (так называемую сингулярность), окруженную горизонтом событий — сферической поверхностью, радиус которой определяется массой и скоростью вращения материи (или моментом импульса), из которой черная дыра сформировалась и из-под которой не может выйти никакой сигнал. Внешний наблюдатель не может получить какую-либо информацию о процессах, происходящих под горизонтом. Но если принять во внимание квантовые эффекты, то оказывается, что черная дыра все-таки может излучать частицы, но этот эффект, как мы увидим ниже, очень слаб и почти всегда может быть проигнорирован.

Черные дыры образуются при сжатии (коллапсе) достаточно массивных звезд на определенных этапах их эволюции либо при столкновении звезд или других черных дыр друг с другом. Массы черных дыр варьируются от нескольких до нескольких миллиардов масс Солнца. Самые массивные черные дыры обычно располагаются в центрах галактик. Есть такая черная дыра и в центре нашего Млечного пути (доказательство ее существования было отмечено прошлогодней Нобелевской премией, см. новость Нобелевская премия по физике — 2020, «Элементы», 13.10.2020).

В 1971 году Стивен Хокинг доказал теорему, утверждающую, что суммарная площадь горизонтов событий всех черных дыр не может уменьшаться со временем, если принимать во внимание любые классические (то есть не квантовые) взаимодействия (S. W. Hawking, 1972. Black holes in general relativity). Это свойство очень напоминает Второе начало термодинамики, которое гласит, что энтропия (часто называемая мерой беспорядка) замкнутой системы тоже является неубывающей с течением времени величиной. Утверждение о том, что у черных дыр есть энтропия и что она пропорциональна площади горизонта, было впервые явно сформулировано Яаковом Бекенштейном (J. D. Bekenstein, 1972. Black holes and the second law). Кроме того, Хокинг показал (S. W. Hawking, 1975. Particle creation by black holes), что черная дыра может излучать частицы (это излучение обычно называют излучением Хокинга), что опять же напоминает термодинамическое поведение нагретого тела. Температура черной дыры определяется следующей формулой:

\[T=\frac{1}{8\pi GM},\]
где \(G\) — это гравитационная постоянная Ньютона, а \(M\) — масса черной дыры. Эта и почти все последующие формулы справедливы для так называемой шварцшильдовской черной дыры, у которой отсутствует момент вращения; у всех реальных черных дыр момент вращения ненулевой, но его учет не меняет картины качественно; также здесь и далее скорость света принята за единицу — это традиционное соглашение в физике частиц и астрофизике. Для черной дыры с массой порядка массы Солнца температура оказывается равной примерно 10−7 кельвин.

Используя закон Стефана — Больцмана, связывающий мощность теплового излучения единицы площади поверхности тела (единицы площади горизонта событий в случае черной дыры) \(J\) с его температурой \(T\):

\[J=\sigma T^4,\]
где \(\sigma\) — это так называемая постоянна Стефана — Больцмана, находим, что время, за которое такая черная дыра излучит всю свою массу (а значит, согласно формуле \(E=mc^2\), — и энергию), составляет приблизительно 1068 лет (для сравнения, возраст Вселенной составляет примерно 1,4·1010 лет), что объясняет возможность пренебречь излучением во всех практических задачах.

Энтропия \(S\) черной дыры, согласно Бекенштейну, связана с площадью ее горизонта событий \(A\) и массой \(M\) так:

\[S=\frac{A}{4G}=4\pi GM^2.\]
Если рассматривать черную дыру с ненулевым моментом импульса \(I\) (это так называемая керровская дыра), то соотношение \(S=\frac{A}{4G}\) остается неизменным, а площадь горизонта событий и температура черной дыры оказываются связанными с \(I\) и \(M\) следующими формулами:

\[A=8\pi G^2M^2\left(1+\sqrt{1-\chi^2}\right),\quad T=\frac{1}{4\pi GM}\frac{\sqrt{1-\chi^2}}{1+\sqrt{1-\chi^2}},\]
где \(\chi=\frac{I}{GM^2}\).

Может показаться, что излучение Хокинга нарушает Второй закон термодинамики для черных дыр, так как в результате этого излучения масса черной дыры, а из-за этого — и площадь ее горизонта событий, уменьшается. Но на самом деле это не так. Второй закон термодинамики утверждает, что энтропия замкнутой системы не может уменьшаться, но в случае излучающего объекта замкнутой системой нужно считать сам источник вместе с его излучением. Сумма их энтропий остается неубывающей величиной, что справедливо также и для излучающей по Хокингу черной дыры.

Помимо очень слабого излучения Хокинга черные дыры могут испускать и другой тип излучения: взаимодействуя с другими макроскопическими объектами, дыра может порождать гравитационные волны. Этот эффект очень похож на излучение электромагнитных волн ускоренно движущимися зарядами с той разницей, что основной вклад в электромагнитное излучение дает изменение дипольного момента системы зарядов, а в гравитационное излучение — квадрупольного. Амплитуда \(\alpha\) гравитационного излучения системы массой \(M\) и характерного размера \(s\), квадрупольный момент которой колеблется с частотой \(\nu\), на расстоянии \(r\gg s\) от нее приблизительно равна

\[\alpha\sim GM\frac{\nu^4s^2}{r}.\]
Гравитационные волны являются волнами геометрии пространства-времени, так что, когда волна проходит по системе из нескольких тел, расстояние между ними немного меняется. Именно это изменение расстояния между объектами и измеряется в гравитационно-волновых экспериментах, для чего удобно ввести величину \(h=\frac{\Delta d}{d}\) (где \(d\) — это расстояние между двумя объектами, а \(\Delta d\) — его изменение из-за гравитационной волны), называемую натяжением (strain).

Из формулы для амплитуды гравитационного излучения видно, что для того, чтобы система излучала гравитационные волны с высокой интенсивностью, колебания в ней должны происходить с большой частотой. Этого проще всего достичь для системы, состоящей из компактных объектов. Лучшим примером такой системы является пара черных дыр, вращающихся друг вокруг друга и в конце концов сливающихся воедино. При этом несколько десятков процентов суммарной массы сливающихся черных дыр может быть преобразовано в гравитационное излучение.

Впервые волны, образовавшиеся в результате слияния пары черных дыр (это событие было обозначено GW150914), были обнаружены гравитационной обсерваторией LIGO в 2015 году (B. P. Abbott et al., 2016. Observation of Gravitational Waves from a Binary Black Hole Merger; см. также новость Гравитационные волны — открыты!, «Элементы», 11.02.2016). Это открытие подтвердило реальность существования гравитационных волн и было удостоено Нобелевской премии по физике 2017 года. Компьютерная симуляция слияния GW150914, основанная на зарегистрированном экспериментом LIGO гравитационно-волновом сигнале, показана на видео:

Приведенная выше формула для амплитуды гравитационного излучения точна в случае достаточно стабильной системы, в которой частота колебаний \(\nu\) и характерный размер \(s\) меняются относительно медленно. Но оба этих условия нарушаются на финальных этапах сближения черных дыр, а потому исследователи вынуждены решать уравнения ОТО численно. В качестве начальных данных вводятся гравитационные поля далеко расположенных друг от друга черных дыр с заданными массами и моментами вращения, которые движутся навстречу друг другу, а дальнейшее их движение и излученные ими гравитационные волны высчитываются на компьютере. Сравнивая расчетные данные со спектром, продолжительностью и интенсивностью гравитационного излучения, которое регистрируется детектором на Земле, можно получить все параметры сближающихся черных дыр.

Аналогично обстоит дело и с образовавшейся большей черной дырой: спектр и интенсивность излучения, генерируемого колеблющимся после слияния горизонтом, моделируются численно, и сравнение расчетов с регистрируемым излучением позволяет найти массу и момент вращения реальной черной дыры.

Событие GW150914 представляло собой слияние двух черных дыр массой около 30 и 35 масс Солнца (по новым данным их массы составляли 31 и 39 масс Солнца, см. A. Ghosh et al., 2021. Constraints on quasinormal-mode frequencies with LIGO-Virgo binary–black-hole observations), произошедшее на расстоянии 1,5 миллиарда световых лет от Земли. Полная энергия излученных гравитационных волн составила около трех солнечных масс, а мощность излучения в течение последних 20 миллисекунд перед слиянием достигала приблизительно 3,6·1049 Ватт, что превышает суммарную мощность светового излучения всех звезд в наблюдаемой Вселенной примерно в 50 раз. Большая часть энергии гравитационных волн была сосредоточена в диапазоне частот от 50 до 250 Гц, а частота обращения черных дыр вокруг центра масс доходила до 75 Гц.

С тех пор как было зарегистрировано событие GW150914, на детекторе LIGO и его аналоге Virgo, расположенном в Италии, было обнаружено еще около 50 подобных событий (A. Ghosh et al., 2021. Constraints on quasinormal-mode frequencies with LIGO-Virgo binary–black-hole observations), но только у одного из них, GW190521, представлявшего собой слияние двух черных дыр с массами примерно 85 и 66 масс Солнца (в только что указанной статье A. Ghosh et al. приводятся другие оценки масс участников слияния: 150 и 120 M⊙), была сопоставимая сила сигнала (R. Abbott et al., 2020. GW190521: A Binary Black Hole Merger with a Total Mass of 150 M⊙, см. также новость Зафиксирован гравитационно-волновой след от рождения черной дыры промежуточной массы, «Элементы», 07.09.2020).

А недавно команда физиков из Массачусетского технологического института (MIT) и других университетов более детально проанализировала данные, собранные LIGO, для того чтобы проверить, справедлива ли теорема Хокинга в действительности, а не только на бумаге. Небольшая статья с их результатами опубликована в свежем выпуске журнала Physical Review Letters. Для этого они подробно изучили весь спектр и интенсивность гравитационных волн, которые были излучены участвовавшими в событии GW150914 черными дырами сначала при их сближении и вращении друг вокруг друга, а затем при формировании третьей черной дыры. Если ОТО, частью которой является теорема Хокинга, верна, то площадь горизонта образовавшейся черной дыры должна быть не меньше суммарной площади горизонтов двух слившихся черных дыр.

Итак, чтобы проверить справедливость теоремы Хокинга, авторы разделили весь полученный сигнал на две части: первая часть соответствует гравитационному излучению при спиралевидном движении двух черных дыр по направлению к центру масс, а вторая — излучению, вызванному колебаниями уже общего горизонта событий (синяя и желтая линии на рис. 2, соответственно).

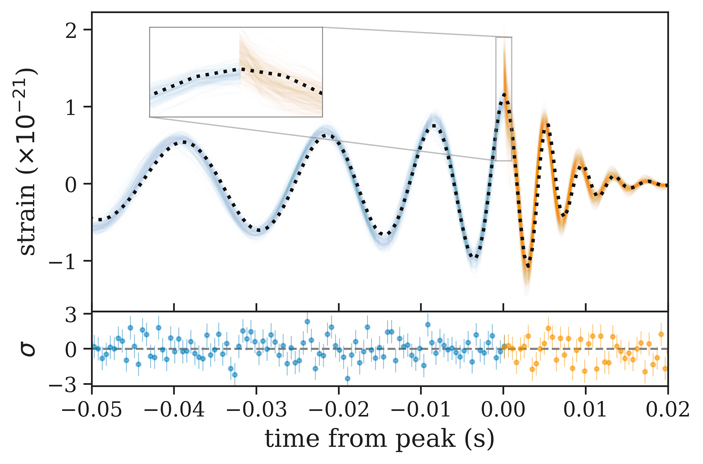
Рис. 2. Измеренное экспериментом LIGO натяжение \(h\) в гравитационной волне от события GW150914. На горизонтальной оси отложено время, за начало отсчета выбран момент соприкосновения горизонтов двух черных дыр. Рисунок из обсуждаемой статьи в Physical Review Letters

Из первой части исследователи извлекли суммарную площадь горизонтов событий двух черных дыр до слияния, которая оказалась приблизительно равна 235 тысячам квадратных километров. Излучение колеблющегося горизонта образовавшейся черной дыры позволило определить его площадь, которая оказалась равна примерно 367 тысячам квадратных километров (для сравнения, площадь территории России составляет около 17 миллионов квадратных километров). Тем самым справедливость теоремы Хокинга подтвердилась на реальных данных. Ученые, естественно, планируют дальнейшие проверки теоремы Хокинга и других законов квантовой механики и термодинамики черных дыр на данных LIGO и его европейского аналога Virgo.

Источник: Maximiliano Isi, Will M. Farr, Matthew Giesler, Mark A. Scheel, and Saul A. Teukolsky. Testing the Black-Hole Area Law with GW150914 // Physical Review Letters. 2021. DOI: 10.1103/PhysRevLett.127.011103.

источник